MVP矩阵推导

其中Model, View的矩阵部分可根据Local转World坐标系转换得到，可参考龙书5.6.1章节。

透视投影矩阵可以分为$x, y$的投影变换，以及$z$的透视校正
首先$x, y$部分可以根据透视变换的相似三角形推导出，此处$x$部分的FOV令为$\theta$，横纵坐标比aspect令为$r=\frac{w}{h}$。

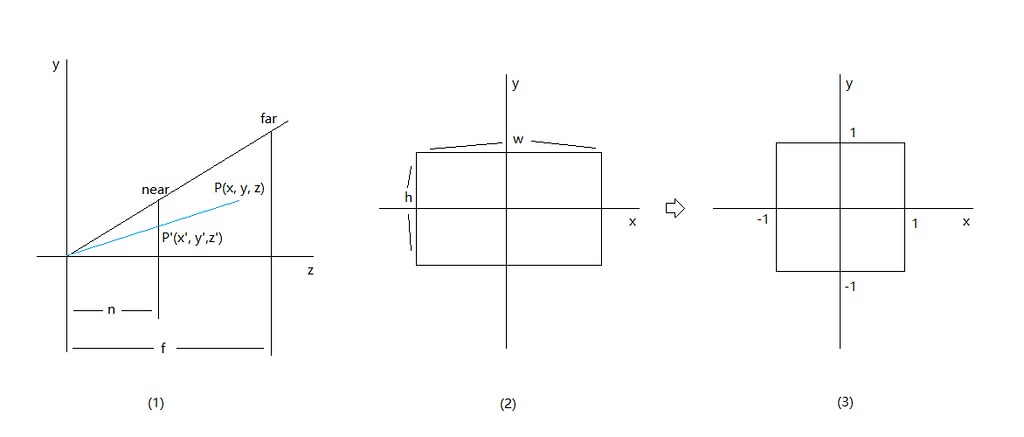
对应$x, y$的转换细节推导可参考透视投影详解

其中$(3)$中的$x'',y''$已经归一化转化到了NDC空间（注意要用$\frac{\theta}{2}$）

$\begin{array}{c}{x}^{\mathrm{\prime }\mathrm{\prime }}=\frac{x}{z}cot\left(\frac{\theta }{2}\right)\frac{1}{r}\\ y^{\mathrm{\prime }\mathrm{\prime }}=\frac{y}{z}cot\left(\frac{\theta }{2}\right)\end{array}$
\begin{array}{l}
x''=\frac{x}{z}cot(\frac{\theta}{2})\frac{1}{r} \\
y''=\frac{y}{z}cot(\frac{\theta}{2})
\end{array}

此时$z$没有做过变换，本质上若需要归一化，也只需要做一个从区间$[n,f]$到$[0,1]$的一个变换即可。但若$z$仅仅只是做了一个区间映射而没有经过透视校正，则会出现下述问题。

---

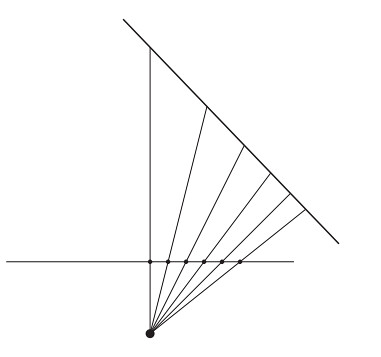
1. Vertex Shader完成顶点变换后需要做光栅化步骤，此时会在投影平面上进行均匀采样。根据上图中，对屏幕上线段进行均匀采样，而其对应线段中的点并非均匀排布。观察发现对应线段上点的$x,y$部分仍然保持均匀分布，但$z$由于透视变换的问题造成结果的畸变。

2. 后续的纹理，颜色插值计算也会因为$z$轴的透视问题带来非均匀分布的问题

本质上的问题是因为$z$在透视变换后，是非线性分布的。因此对应的解决方案就是找到一个能够满足深度前后关系不变，且能支持线性插值的量来代替原有的$z$。

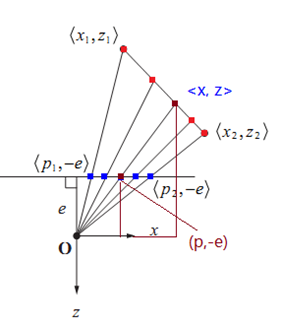
此处证明$\frac{1}{z}$是线性分布的。令直线为$ax+bz=c$，给出线段上一点$[x, z]$，其对应投影平面上的点为$[p, -e]$，即有

$\begin{array}{c}\frac{p}{x}=\frac{-e}{z}\\ (-\frac{ap}{e}+b)z=c\\ \frac{1}{z}=-\frac{ap}{ce}+\frac{b}{c}\end{array}$
\begin{array}{l}
\frac{p}{x} = \frac{-e}{z} \\
(-\frac{ap}{e}+b)z = c \\
\frac{1}{z} = -\frac{ap}{ce}+\frac{b}{c}
\end{array}

设线段的头尾点为$[x_1, z_1], [x_2, z_2]$以及对应投影平面上的点为$[p_1,-e],[p_2,-e]$。令$p_3=(1-t)p_1+tp_2$由$p_1,p_2$线性插值得出，求$[p_3,-e]$对应的线段上的点。

$\begin{array}{ccc}\frac{1}{z_3}& =& -\frac{a{p}_3}{ce}+\frac{b}{c}\\ & =& -\frac{a{p}_1}{ce}(1-t)--\frac{a{p}_2}{ce}t+\frac{b}{c}\\ & =& (-\frac{a{p}_1}{ce}+\frac{b}{c})(1-t)+(-\frac{a{p}_2}{ce}+\frac{b}{c})t\\ & =& \frac{1}{z_1}(1-t)+\frac{1}{z_2}t\end{array}$
\begin{array}{l}
\frac{1}{z_3} & = & -\frac{ap_3}{ce}+\frac{b}{c} \\
& = & -\frac{ap_1}{ce}(1-t)–\frac{ap_2}{ce}t+\frac{b}{c} \\
& = & (-\frac{ap_1}{ce}+\frac{b}{c})(1-t)+(-\frac{ap_2}{ce}+\frac{b}{c})t \\
& = & \frac{1}{z_1}(1-t)+\frac{1}{z_2}t
\end{array}

可见$\frac{1}{z}$在直线上可以线性插值。由于$z$轴在光栅化中需要被插值，因此直接构造$\frac{1}{z}$使得硬件在做插值时保持线性，为了将$z'$归一化到$[0,1]$需要构造$z'=A+\frac{B}{z}+B$。已知

$\begin{array}{ccc}0& =& A+\frac{B}{n}\\ 1& =& A+\frac{B}{f}\end{array}$
\begin{array}{l}
0 & = & A+\frac{B}{n} \\
1 & = & A+\frac{B}{f}
\end{array}

求解方程组，则有$A=\frac{f}{f-n}, B=\frac{nf}{f-n}$

可得最终透视投影矩阵

这里推导的结果为左手系。若左右手系区分则只需要调换部分元素位置，可见龙书推导。

$\left[\begin{array}{cccc}\frac{1}{rtan\left(\frac{\theta }{2}\right)}& 0& 0& 0\\ 0& \frac{1}{tan\left(\frac{\theta }{2}\right)}& 0& 0\\ 0& 0& \frac{f}{f-n}& 1\\ 0& 0& \frac{nf}{f-n}& 0\end{array}\right]$
\left[
\begin{matrix}
\frac{1}{rtan(\frac{\theta}{2})} & 0 & 0 & 0 \
0 & \frac{1}{tan(\frac{\theta}{2})} & 0 & 0 \\
0 & 0 & \frac{f}{f-n} & 1 \\
0 & 0 & \frac{nf}{f-n} & 0
\end{matrix}
\right]

Sophia Renderer上的矩阵

由于DirectX 11的GPU部分采用了列主的矩阵排布。一般有两种解决方案

1. CPU端采用行主，GPU端采用列主，在CPU绑定矩阵到CB的时候转置一次。
2. CPU端采用行主不变，GPU端直接左乘向量(GPU上的矩阵是CPU的转置)

采用两种方式不同的地方在于，前者$MVP=Projection$ View World Vector，后者本质上是$MVP = Vector World^T$ View^T Projection^T，而由于列主是默认的，因此在GPU上看起来就像$MVP = V$ W V * P一样。本质上只是CPU端的转置结果。

这里Sophia Renderer采用第二种方式，即默认GPU端都为CPU端绑定结果的转置，因此选用左乘来得到正确结果。

Reference

1. Mathematics for 3D Game Programming and Computer Graphics, Third Edition, Section 5.4
2. Introduction to 3D GAME PROGRAMMING WITH DIRECTX® 11, Section 5.6